Mathematical reasoning: And, or and not

Logic is very important in programming. We use ||, && and ! many times while programming. But do we really understand it? Mathematical reasoning or the principle of mathematical reasoning is a part of mathematics where we determine the truth values of the given statements. It may or may not help you, but is a valuable thing to learn. This post is a bit basic but in the next posts, we will cover more concepts like De Morgan's Theorem and many other things. I made most of the diagrams myself, so hope you like them.😀

And

What is And? In JavaScript, we write and like this: &&. In Maths, the symbol of And is ∧. So what does and really means🤔.

In mathematical reasoning, we use Venn diagrams to depict something. So in this Venn diagram, we have 2 conditions, p and q.

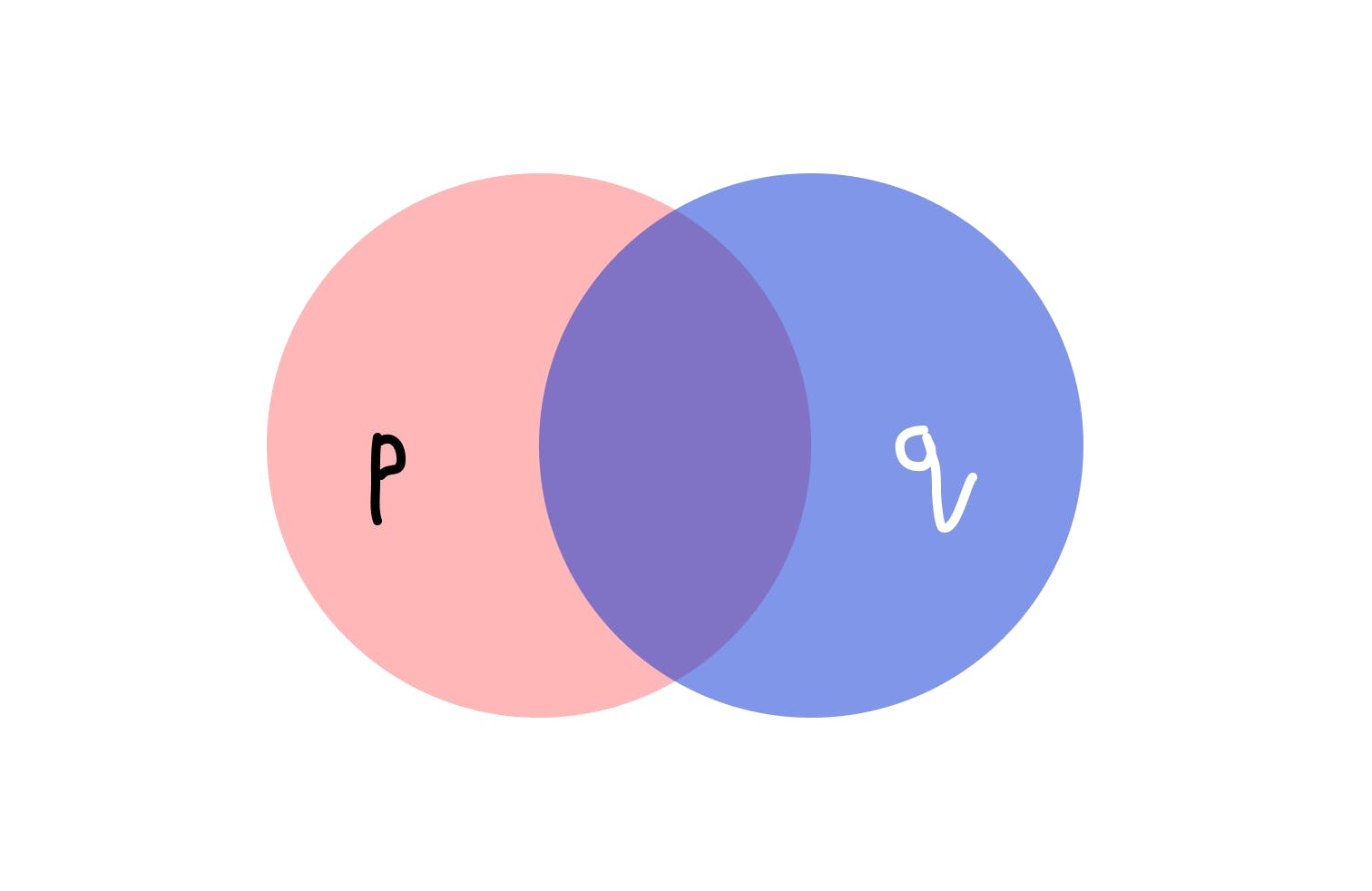
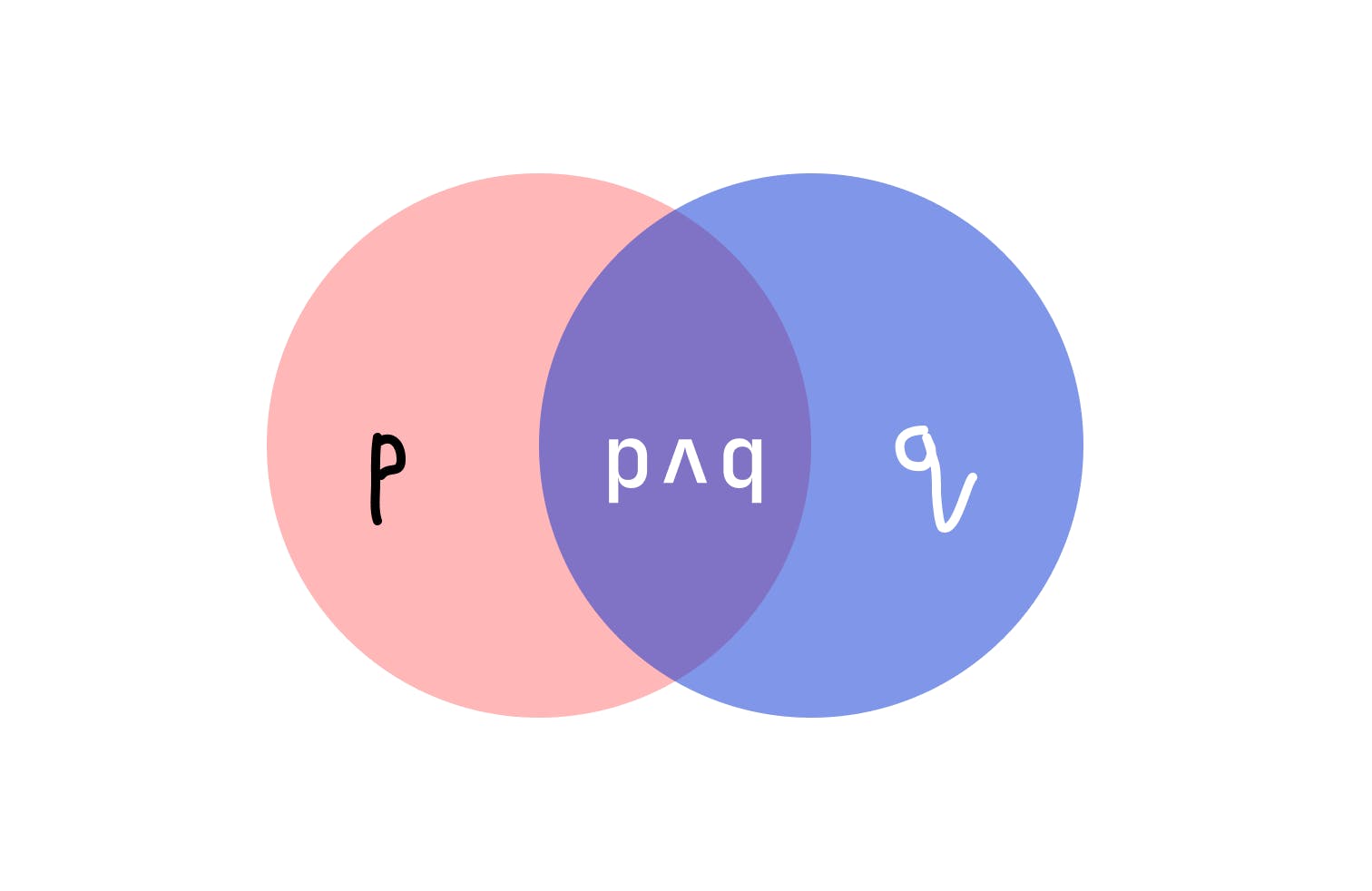
So what should be p && q. Think about it. p && q means the place where p and q, both are there. In Venn diagrams, it means the intersection of the 2 conditions.

Truth table of And

Here's the truth table of And:

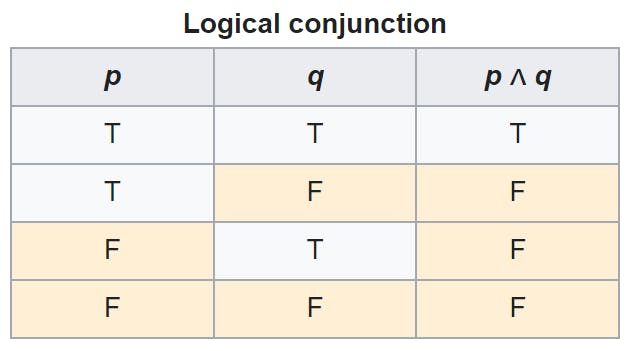
And is true only when both the conditions, p & q are true. In Venn, true is the whole rectangle in which p and q are there and false means nothing. I will discuss more it in a future blog post.

So to make p && q true, which means the intersection of p && q true, both p and q should be true.

Or

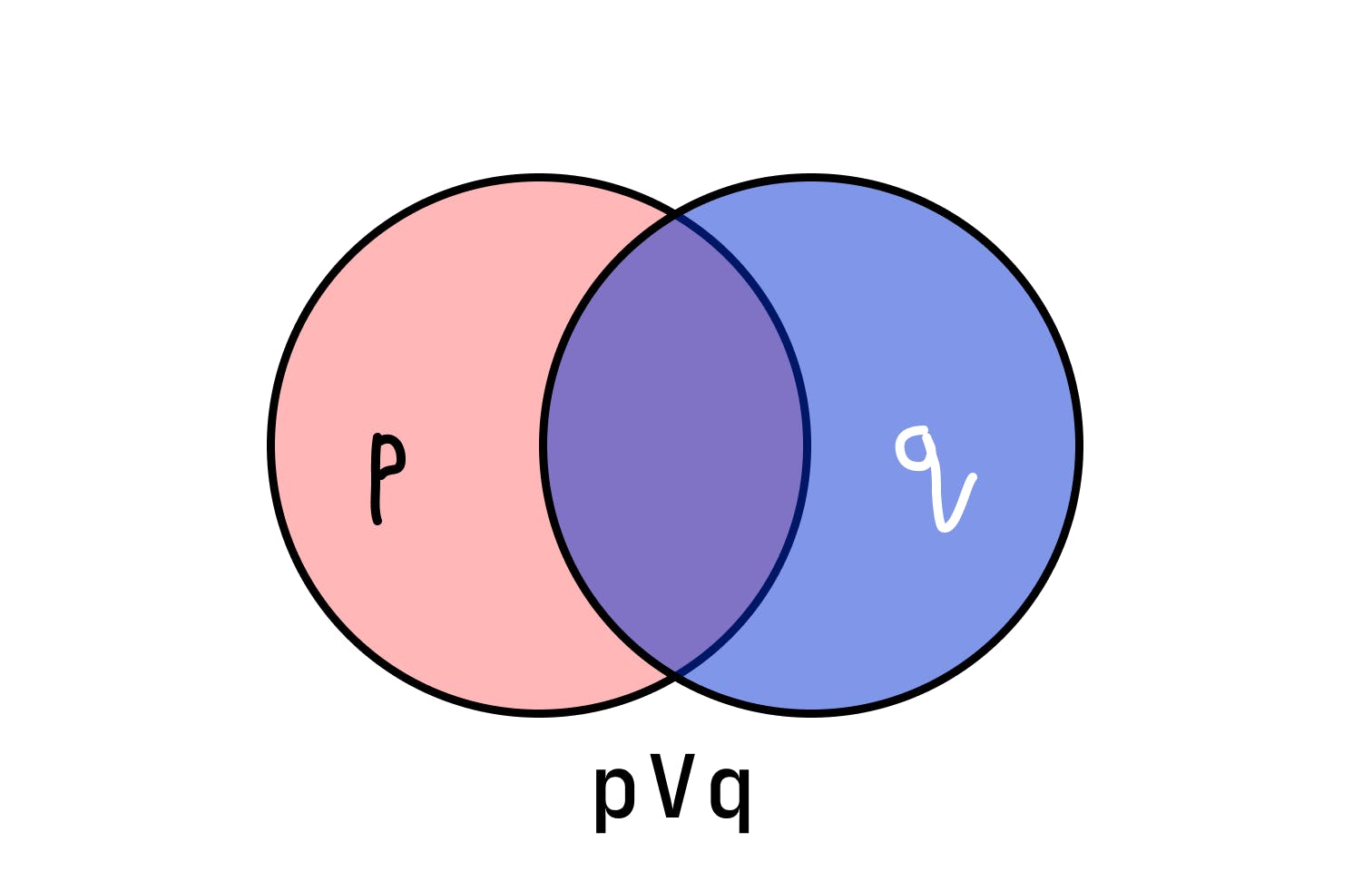
What is Or? In JavaScript, we write and like this: ||. In Maths, the symbol of And is V. So what does and really means🤔.

So what should be p || q. Think about it. p || q means the combination of p and q.

Truth table of Or

Here's the truth table of Or:

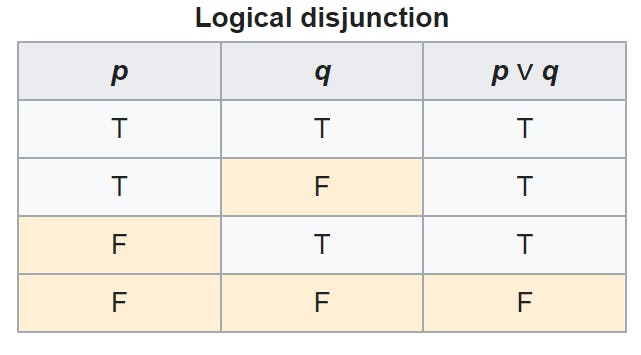
Or is true when one of the conditions is true.

So to make p || q true, either p or q should be true.

Not

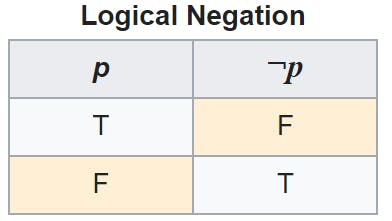
What is Not? In JavaScript, we write and like this: !. In Maths, the symbol of Not is ~. So what does and really means🤔.

So what should be !p. Think about it. !p means something that is not p.

Truth table of Not

Here's the truth table of Not: